BLOG
音声活用ブログ
次回説明するネメシスコ社の保有する特許を理解する為には音声の周波数分析に関する知識が必要です
2021.04.23
テクノロジー
テーマ:
12 音声の周波数分析
次回No.13とNo.14のブログにてネメシスコ社の保有する特許について解説します。それを理解する為には音声の周波数分析に関する知識が必要なので、これを簡単に分かり易く説明します。
音声波形
音声については以前のブログNo.6及びNo.7の「音声の性質」でも説明していますが、音圧(鼓膜にかかる空気の圧力)の時間的な変化の事を言います。(図1)

これを良く見ると、繰り返しのパターンがあることがわかります。繰り返しの時間を「周期」、繰り返しのことを「周期性がある」、1秒間に表れる繰り返しの回数を「周波数」または「振動数」と言います。周波数はヘルツという単位で表され、1秒間に同一パターンが何回繰り返されるかを意味します。実は音声波形に含まれる繰り返しのパターンは1つではなく、周波数の異なる多くのパターンが含まれます。どのような繰り返しパターンがどれだけの割合で含まれているかの情報を取り出すことを周波数分析と言います。
純音(正弦波)
図1では繰り返しパターンの形状が乱雑な波形になっておりパターン形状を簡単に表現することが出来ません。そこで乱雑な波形を簡単な繰り返し波形の重ね合わせで示します。乱雑な波形の音声を「複合音」、単純な繰り返し波形の音声を「純音」と言い表します。純音は音叉から出る音の事です。純音は数学的には正弦波と言い図2に示すようなお椀の形をした波形が連続しているもので、音叉をたたいた時に発する空気の圧力の変化を時間的に表すとこの形になります。この縦軸は音の強さ(音圧の強さ)すなわち空気の圧力、あるいは空気の圧力値をマイクロホンで変換した電圧値を表し、横軸は時間を表します。波形の周期の間隔が短いほど高い周波数を表しています。横軸がつまっていれば周波数は高いですし、間隔が開いていれば周波数は低いことになります。この波形について数学的には三角関数の一種であるサイン(sin)関数あるいはコサイン(cos)関数で表すことができます。

三角関数の復習
三角関数は高校の数学で習ったと思いますが、昔のことでもう忘れている人も多いと思います。周波数分析を理解するには三角関数の理解が不可欠ですから少し復習してみましょう。三角関数の最も代表的な例はサイン関数で$y=\sin\theta$ と書きます。(ここで$\theta$ はギリシャ語のシータと呼びます。)この定義は図3に示すように原点oを中心とした半径1の円上に点Pを$x$ 軸と直線OPが角度$\theta$ をなすように取り、Pから$x$ 軸に下した直線が$x$ 軸と交わる点をHとして、PHの長さを$\sin\theta$ と定義します。

この定義からわかるように角度$\theta$ は0°から360°まで取る事ができます。しかし周波数分析を行う時の角度の数え方として「°」では無く、ラジアンと言う記法を用います。ラジアンと言うのは度の代わりに半径1の円の弧の長さを使って角度を表現することです。図3では$\theta$ の値を表すのに 軸から点Pまでの弧の長さを用います。円周率(3.141592…)をギリシャ文字の$\pi$(パイと呼びます)と表記すると半径1の円の円周は$2\pi$ですから角度360°はラジアン記法で角度$2\pi$ラジアンとなり、角度90°は$\pi/2$になります。サイン関数とラジアン記法の定義から
$$\hspace{0mm}\sin0=0, \sin(\frac{\pi}{2})=1, \sin(\pi)=0, $$
$$\sin(\frac{3\pi}{2})=-1, \sin(2\pi)=0$$
となります。$\theta$ が30°の場合にはラジアン記法では$\theta=\pi/6$ です。この場合は
$$\sin\frac{\pi}{6}=\frac{1}{2}$$
になります。ここでラジアン記法の定義を拡張してラジアンの値を0から$2\pi$に限定せず、どのような実数でも取れるようにし、これをラジアン値$r+2\pi$ を$r$ と読み替えることにします。こうしますと$\theta$ は任意の値が取れます。そこで$\theta$ を横軸に、$\sin\theta$ を縦軸に描くと図4のようになります。

この図からわかるように$\sin\theta$ は最大値が$1$で最小値が$-1$です。1周期は$2\pi$ で$\theta$ の値が$2\pi$ を超えると波形が繰り返されます。
純音波形のサイン関数による表し方
では次にサイン関数を用いて純音の波形を描いてみましょう。これを図5に示します。

横軸は$\theta$ の代わりに時間$t$ (秒)を用います。縦軸は音圧を表します。音圧の最大値を$P_{m}$ と書くこととし、例えば2ミリパスカルとします。周期を$T$(秒)と書くこととし、純音の周波数を500ヘルツ(すなわち1秒間に500回の繰返し)としますと繰り返しの周期は1/500秒になりますので$T=0.002$ 秒になります。このときの音をサイン関数で表すと
$$P=P_{m}\sin(\frac{2\pi}{T}t) \hspace{20mm}(1)$$
となります。例えた数字を当てはめると
$$P=2\sin(\frac{2\pi}{0.002}t) \hspace{20mm}(1)’$$
となり、サイン関数$\sin\theta$ の$\theta$ の代わりに$(2\pi/T)t$ を用いています。これは何故かと言うと、(1)式の周期をサイン関数$\sin\theta$ の周期である$2\pi$ と一致させる為です。時間変数$t$ が1周期の時刻すなわち$t=T$ の時に
$$\frac{2\pi}{T}t=\frac{2\pi}{T}T=2\pi$$
となり$2\pi$ と一致します。
ここで周波数分析に使う記号を紹介しておきます。
$$\hspace{10mm} 周波数\hspace{15mm}f=\frac{1}{T} (\frac{1}{秒})$$
$$\hspace{10mm}角周波数\hspace{10mm}\omega=2\pi f=\frac{2\pi}{T} (\frac{1}{秒})$$
周波数$f$ (英語のfrequencyの頭文字)の単位はヘルツで1秒間あたりの繰返し回数です。周波数に$2\pi$ を掛けたものは角周波数と言ってギリシャ語のオメガ$\omega$ で表します。1秒間の繰返し回数を1回あたり$2\pi$ と数えます。これを使いますと$(1)$ の式は
$$\hspace{20mm}P=P_{m}\sin(2\pi ft) \hspace{20mm} (2)$$
あるいは
$$\hspace{20mm}P=P_{m}\sin(\omega t)\hspace{25mm} (2)’$$
と表すことができます。
波形の重ね合わせ
次に、非常に大切な波形の性質をご紹介します。どれだけ乱れた波形であっても正弦波の重ね合わせで表記できるということです。これはフランスのジョセフ・フーリエ男爵(写真)が19世紀初頭に発見し、数学的な理論を確立したものでフーリエ解析と呼ばれています。
下の図を参照して下さい。
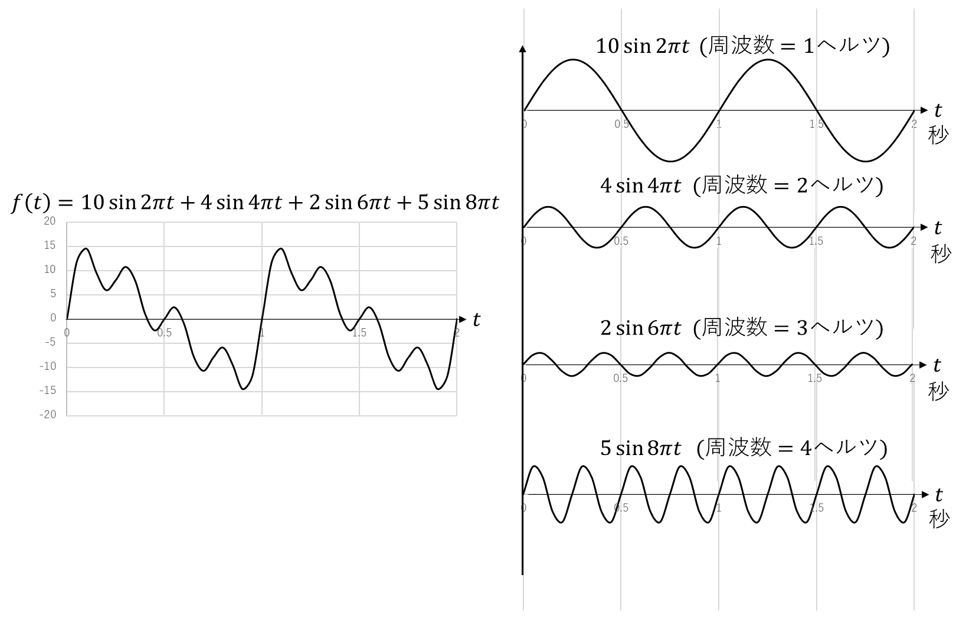
左側の波形は少し乱れていますが、これは右側の4つの正弦波(サイン関数)を単純に足し合わせたもので、右側の一番上の正弦波は大きさが10で周期が1秒(周波数は1ヘルツ)、2番目の正弦波は大きさが4で周期が0.5秒(周波数は2ヘルツ)、3番目の正弦波は大きさが2で周期が1/3秒(周波数3ヘルツ)、4番目の正弦波は大きさが5で周期が0.25秒(周波数4ヘルツ)です。この場合左側の乱れた波形を時間の関数$f(t)$ とすると数学的には次のように表現します。
$$f(t)=10\sin2\pi t+4\sin4\pi t+2\sin6\pi t+5\sin8\pi t$$
このとき各項の正弦波の大きさ(この場合には10、4、2、5)が大切でこれを各周波数に対応する成分と言います。この成分と周波数との対応表あるいはグラフのことを周波数分析表あるいは周波数分析グラフと言いこの例では下記の表及び図7になります。
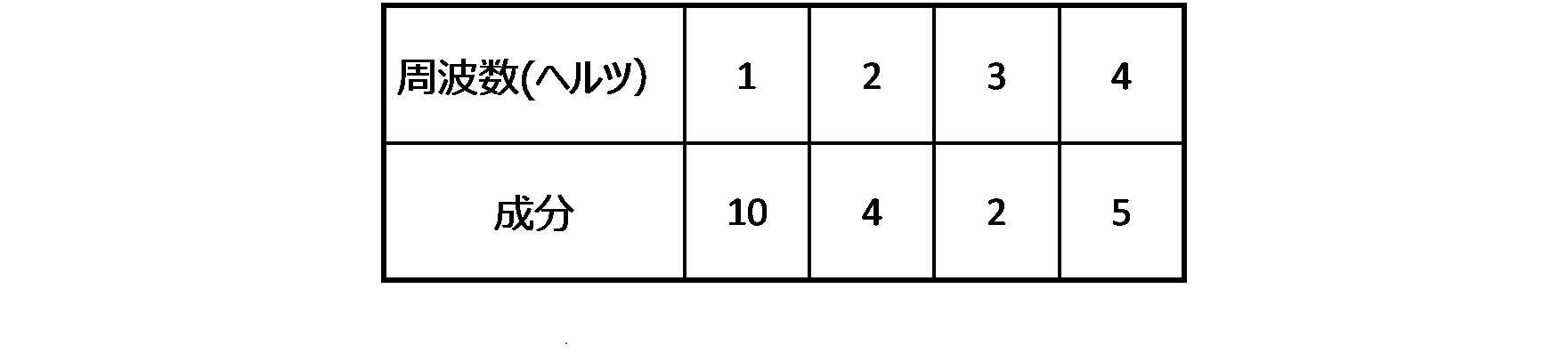

これを周波数分析と言います。すなわち乱れた波形はいろいろな周波数をもつ正弦波がどのくらいの重みで足し算されているかを示したもので、上記の例では周波数1.0ヘルツの正弦波の成分は10、周波数3.0ヘルツの成分は2.0であると表現します。別の言い方をすれば、もともとの波形の中のいろいろな周波数の正弦波の分布の度合いを示していることになります。分布の度合いのことを英語でスペクトラムと言い、周波数分析はスペクトラム分析とも言われます。
なぜ周波数分析は重要か?
周波数分析は理工学のあらゆるところで使われていますが、その理由は振動を伴うあらゆる現象には波形があり、波形を調べる時に強力な道具になるからです。人間の声は空気の振動であり、波形そのものです。音声に含まれる感情情報も声の周波数成分と相関があり、これを知ることにより感情情報を得ることができるからです。ネメシスコ社の特許では声の周波数分析と感情情報の例が記載されています。
以上
関連記事
ピックアップ
- CATEGORY
- Nemesysco社
- コールセンター
- 感情解析ラボ(活用事例)
- 不正防止
- 金融機関
- 保険金詐欺
- ストレス
- お知らせ
- テクノロジー
- マーケット
- 人気記事
- 11 音声は何を伝えているか?
- 40 用途が拡がる音声感情解析ソリューション (聞き手理解確認ソリューションについて2)
- 19 音声感情分析(解析)で明らかになったプレゼンの極意
- 50 なぜ音声から感情がわかるのか(3)
- 1 LVAテクノロジー (1)
テーマ
- 感情
- パスカル
- 等ラウドネス曲線
- 音の性質
- デシベル
- 音速
- 周波数
- LVA
- フォーマント
- 解析
- コールセンター
- 運営効率
- パーソナリティー
- 性格診断
- オペレーター感情
- モチベーション
- コールセンター運営
- サイエンスラボ
- 音声解析研究
- 応対品質
- 基盤技術
- ビジネス予測
- 感情解析ビジネス
- 米国心理学会
- 発声機構
- 聴覚機構
- 米国特許
- 学術論文
- 周波数分析
- Nemesysco
- ネメシスコ
- 人事面接
- 聞き手。理解度、音声感情解析
- 聞き手
- 理解度
- パーソナルキャラクター
- ソーシャルスタイル
- DISC理論
- メタバース
- 音声感情
- AI
- コールセンター、品質管理
- 音声感情解析
- 期待効用理論、効用関数
- ベルヌーイ
- ESAS
- 感情解析ラボ
- プロスペクト理論
- 価値関数
- 言語
- 不随意感情情報
- 意図的感情情報
- 音声感情解析、AI、機械学習
- 音の波形
- フーリエ変換
- Chat-GPT、AI、感情、音声
- 警察
- 情報機関
- 人事部門
- 面接
- 採用
- ストレスチェック
- リモートミーティング
- ロボット
- エンタメ
- カラオケ採点
- 学習理解度把握
- 愛情チェック
- 役割
- 機能
- 教育、中国、学習量、学習効率
- 保険請求
- 不正申告
- 保険
- 詐欺
- アレクサ
- Alexa
- amazon
- アマゾン
- 住民感情、コロナ、自治体
- エモーションロジック
- 不正請求
- 保険金詐欺
- Insurance Fraud
- 保険金
- Voice Screen
- ストレス